Soru Sor
Sorunu sor hemen cevaplansın.
# Düzlemsel Nedir # Düzlemsel Bölgelerin Alanları Nasıl Hesaplanır # Karesel Bölgenin Alanı Nasıl Hesaplanır # Dikdörtgensel Bölgenin Alanı Nasıl Hesaplanır # Üçgensel Bölgenin Alanı Nasıl Hesaplanır # Küpün Alanı Nasıl Hesaplanır # Dikdörtgenler Prizmasının Alanı Nasıl Hesaplanır # Kare Prizmanın Alanı Nasıl Hesaplanır
Aşağıda verilen şeklin alanını bulalım.


ÖRNEK:
Çözüm:
Renkli alan ABCD dikdörtgeninin alanından AFC ve FBE üçgenlerinin alanları toplamının çıkarılması ile bulunur.Yani
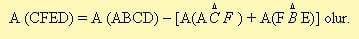
Buna göre ABCD dikdörtgeninin alanı;
AC x AB dir.
AC = 7 cm AB = 3 + 8 = 11 cm
7 x 11 = 77 santimetre kare olur.
ACF üçgeninin alanı :
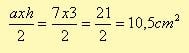
FBE üçgeninin alanı:
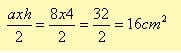
İki üçgenin alanlarını toplayıp, dikdörtgenin alanından çıkarırız.

Yukarıdaki küpün alanı görüldüğü gibi 6 birim karedir.
ÖRNEK:
Bir ayrıtının uzunluğu 12 dm olan bir küpün alanı kaç santimetre karedir?
Çözüm:
Bir küpte 6 tane kare şeklinde yüz vardir.
a= 8 dm = 80 cm olur.
Karenin alanı a x a olduğundan 80 x 80 = 6400 (bir karenin alanı)
6400 x 6 = 38 400 santimetrekare (küpün alanı)
ÖRNEK:
Alanı 150 santimetrekare olan küpün bir kenarının uzunluğu kaç cm olur?
Çözüm:
Küpün birbirine eşit 6 yüzü olduğundan verilen alanı önce 6′ya böleriz.
150:6=25
a x a =25 ise
a = 5 cm olur. (ayrıt uzunluğu)
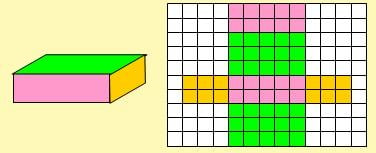
Yukarıdaki dikdörtgenler prizmasının alanı 62 birim karedir.
Bir dikdörtgenler prizmasında 2′şer 2′şer eş olmak üzere 3 çeşit dikdörtgen bulunur.
ÖRNEK:
a = 5 cm
b = 2 cm
c = 8 cm olan dikdörtgenler prizmasının alanı kaç santimetrekaredir?
A = 2(axb) + 2(axc) + 2(bxc)
A = 2(5×2) + 2(5×8) + 2(2×8)
A = (2×10) + (2×40) + (2×16)
A = 20 + 80 + 32
A = 132 santimetrekare (prizmanın alanı)
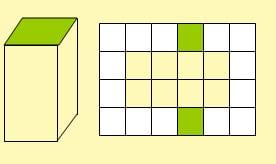
Yukarıdaki prizmanın alanı 10 birim karedir.
ÖRNEK:
Taban ayrıtı 7 cm ve yüksekliği 12 cm olan prizma şeklindeki bir kutuyu kaplamak için ne kadar kağıt gerektiğini bulunuz.
Çözüm:
Prizmada kare şeklinde 2 tane taban ve dikdörtgen şeklinde 4 tane yanal yüz olduğundan;
A = 2(a x a) + 4(a x h(b)) dir.
a= 7 cm
h(b) = 12 cm verilmiş.Verilenleri yerlerine yerleştirirsek
A = 2(7×7) + 4(7×12)
A= (2×49) + (4×94)
A = 98 + 376
A = 474 santimetrekare olur.
ALIŞTIRMA:
Aşağıda verilen blokun yüzey alanını hesaplayınız.
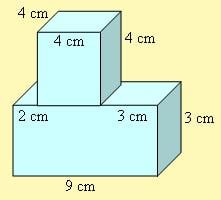
Üstteki prizma ölçülerinden de anlaşılacağı gibi bir küptür.Sadece alt tabanı, alttaki prizmaya çakıştığı için hesaplanması gereken 5 yüzü vardır.Bu nedenle
5(a xa)
5(4 x4)= 5 x 16= 80 (üstteki küpün alanı)
Altta verilen dikdörtgenler prizmasının boyutları
a=9 cm
b=3 cm
c=4 cm olur.(c kenarı aynı zamanda küpün kenar uzunluğudur.)Buna göre
2(axb) + 2(axc) + 2(bxc) prizmanın alanını verir.
2(9×3) + 2(9×4) + 2(3×4)=
2×27 + 2×36 + 2×12=
54 + 72 + 24=150 santimetrekare(tüm alan olur.)
Ancak küpün oturduğu alanı tüm alandan çıkarırsak
150 – (4×4) =
150 – 16 =134 (dikdörtgenler prizmasının alanı)
Blokun alanı = küp +dikdörtgenler prizması
Blokun alanı = 80 + 134 = 214 santimetrekaredir.
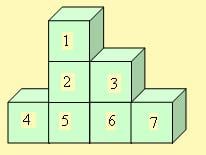
Yukarıda küplerden meydana gelmiş olan blokun alanını hesaplayalım.
a = 5 cm
1 numaralı küpün sadece alt tabanı görünmüyor.Yani 5 yüzün alanı hesaplanacak.Bir yüzün alanı 5×5 = 20
5 yüzün alanı 20 x 5 = 100 santimetrekare(1 nolu küpün alanı)
2 numaralı küpün alt ve üst tabanları ile bir yan yüzü görünmüyor.Dolayısı ile 3 yüzünün alanı hesaplanır.
3 x 20 = 60 santimetrekare(2 nolu küpün alanı)
3 numaralı küpün alt tabanı ve 1 yan yüzü görünmüyor.Dolayısı ile 4 yüzünün alanı hesaplanır.
4 x 20 = 80 santimetrekare(3 nolu küpün alanı)
4 ve 7 numaralı küplerin sadece birer yan yüzleri çakışık olduğundan 5′er yüzleri hesaplanır.
5 x 20 = 100
2 x 100 = 200 santimetrekare(4 ve 7 nolu küplerin toplam alanı)
5 ve 6 numaralı küplerin de üst taban ve 2′şer yanal yüzleri çakışık olduğundan 3′er yüzlerinin alanı hesaplanır.
3 x 20 = 60
2 x 60 =120 santimetrekare(5 ve 6 nolu küplerin toplam alanı)
En son olarak tüm küplerin alanlarını toplarız.
100 + 60 + 80 + 200 + 120 = 560 santimetrekare
Tarih: 2013-11-06 22:00:00 Kategori: Edebiyat
Soru Tarat
Kitaptan sorunu tarat hemen cevaplansın.
Sorunu sor hemen cevaplansın.
Düzlemsel Nedir
Bu Yazıda Neler Var:
Düzlemsel Nedir
Düzlemsel, yani aynı düzlem içinde bulunan noktaların oluşturduğu geometrik şekillere verilen ad. Düzlemsel şekiller deyince akla Doğru, açı, üçgen, dörtgen, paralelkenar, eşkenar dörtgen, dikdörtgen, kare, yamuk, deltoid, beşgen, düzgün beşgen, altıgen, düzgün altıgen , çokgenler, çember, elips sık kullanılan düzlemsel geometrik şekillerdir.
Düzlemsel Bölgelerin Alanları Nasıl Hesaplanır
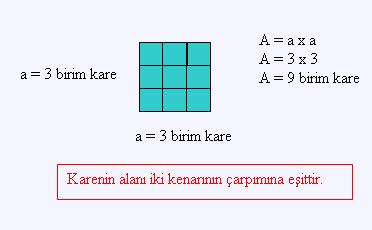
Karesel Bölgenin Alanı Nasıl Hesaplanır

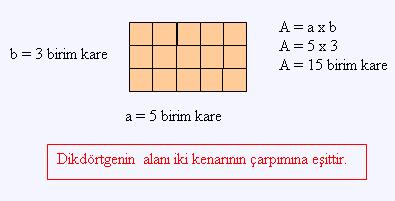
Dikdörtgensel Bölgenin Alanı Nasıl Hesaplanır


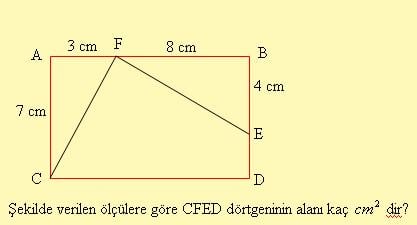
Aşağıda verilen şeklin alanını bulalım.

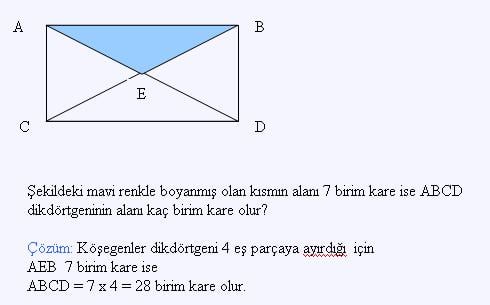
Üçgensel Bölgenin Alanı Nasıl Hesaplanır
Dik üçgenin alanı; taban kenarı ile yüksekliğinin çarpımının ikiye bölünmesi ile bulunur.
ÖRNEK:

Çözüm:
Renkli alan ABCD dikdörtgeninin alanından AFC ve FBE üçgenlerinin alanları toplamının çıkarılması ile bulunur.Yani
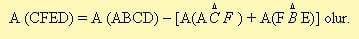
Buna göre ABCD dikdörtgeninin alanı;
AC x AB dir.
AC = 7 cm AB = 3 + 8 = 11 cm
7 x 11 = 77 santimetre kare olur.
ACF üçgeninin alanı :
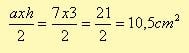
FBE üçgeninin alanı:
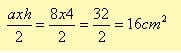
İki üçgenin alanlarını toplayıp, dikdörtgenin alanından çıkarırız.

Küpün Alanı Nasıl Hesaplanır
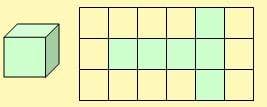
Bir küpün açılımını kareli zemine yerleştirelim.
Yukarıdaki küpün alanı görüldüğü gibi 6 birim karedir.
ÖRNEK:
Bir ayrıtının uzunluğu 12 dm olan bir küpün alanı kaç santimetre karedir?
Çözüm:
Bir küpte 6 tane kare şeklinde yüz vardir.
a= 8 dm = 80 cm olur.
Karenin alanı a x a olduğundan 80 x 80 = 6400 (bir karenin alanı)
6400 x 6 = 38 400 santimetrekare (küpün alanı)
ÖRNEK:
Alanı 150 santimetrekare olan küpün bir kenarının uzunluğu kaç cm olur?
Çözüm:
Küpün birbirine eşit 6 yüzü olduğundan verilen alanı önce 6′ya böleriz.
150:6=25
a x a =25 ise
a = 5 cm olur. (ayrıt uzunluğu)
Dikdörtgenler Prizmasının Alanı Nasıl Hesaplanır
Bir dikdörtgenler prizmasının açılımını kareli zemine yerleştirelim.
Yukarıdaki dikdörtgenler prizmasının alanı 62 birim karedir.
Bir dikdörtgenler prizmasında 2′şer 2′şer eş olmak üzere 3 çeşit dikdörtgen bulunur.
ÖRNEK:
a = 5 cm
b = 2 cm
c = 8 cm olan dikdörtgenler prizmasının alanı kaç santimetrekaredir?
A = 2(axb) + 2(axc) + 2(bxc)
A = 2(5×2) + 2(5×8) + 2(2×8)
A = (2×10) + (2×40) + (2×16)
A = 20 + 80 + 32
A = 132 santimetrekare (prizmanın alanı)
Kare Prizmanın Alanı Nasıl Hesaplanır
Bir kare prizmanın açılımını kareli zemine yerleştirelim.
Yukarıdaki prizmanın alanı 10 birim karedir.
ÖRNEK:
Taban ayrıtı 7 cm ve yüksekliği 12 cm olan prizma şeklindeki bir kutuyu kaplamak için ne kadar kağıt gerektiğini bulunuz.
Çözüm:
Prizmada kare şeklinde 2 tane taban ve dikdörtgen şeklinde 4 tane yanal yüz olduğundan;
A = 2(a x a) + 4(a x h(b)) dir.
a= 7 cm
h(b) = 12 cm verilmiş.Verilenleri yerlerine yerleştirirsek
A = 2(7×7) + 4(7×12)
A= (2×49) + (4×94)
A = 98 + 376
A = 474 santimetrekare olur.
ALIŞTIRMA:
Aşağıda verilen blokun yüzey alanını hesaplayınız.

Üstteki prizma ölçülerinden de anlaşılacağı gibi bir küptür.Sadece alt tabanı, alttaki prizmaya çakıştığı için hesaplanması gereken 5 yüzü vardır.Bu nedenle
5(a xa)
5(4 x4)= 5 x 16= 80 (üstteki küpün alanı)
Altta verilen dikdörtgenler prizmasının boyutları
a=9 cm
b=3 cm
c=4 cm olur.(c kenarı aynı zamanda küpün kenar uzunluğudur.)Buna göre
2(axb) + 2(axc) + 2(bxc) prizmanın alanını verir.
2(9×3) + 2(9×4) + 2(3×4)=
2×27 + 2×36 + 2×12=
54 + 72 + 24=150 santimetrekare(tüm alan olur.)
Ancak küpün oturduğu alanı tüm alandan çıkarırsak
150 – (4×4) =
150 – 16 =134 (dikdörtgenler prizmasının alanı)
Blokun alanı = küp +dikdörtgenler prizması
Blokun alanı = 80 + 134 = 214 santimetrekaredir.

Yukarıda küplerden meydana gelmiş olan blokun alanını hesaplayalım.
a = 5 cm
1 numaralı küpün sadece alt tabanı görünmüyor.Yani 5 yüzün alanı hesaplanacak.Bir yüzün alanı 5×5 = 20
5 yüzün alanı 20 x 5 = 100 santimetrekare(1 nolu küpün alanı)
2 numaralı küpün alt ve üst tabanları ile bir yan yüzü görünmüyor.Dolayısı ile 3 yüzünün alanı hesaplanır.
3 x 20 = 60 santimetrekare(2 nolu küpün alanı)
3 numaralı küpün alt tabanı ve 1 yan yüzü görünmüyor.Dolayısı ile 4 yüzünün alanı hesaplanır.
4 x 20 = 80 santimetrekare(3 nolu küpün alanı)
4 ve 7 numaralı küplerin sadece birer yan yüzleri çakışık olduğundan 5′er yüzleri hesaplanır.
5 x 20 = 100
2 x 100 = 200 santimetrekare(4 ve 7 nolu küplerin toplam alanı)
5 ve 6 numaralı küplerin de üst taban ve 2′şer yanal yüzleri çakışık olduğundan 3′er yüzlerinin alanı hesaplanır.
3 x 20 = 60
2 x 60 =120 santimetrekare(5 ve 6 nolu küplerin toplam alanı)
En son olarak tüm küplerin alanlarını toplarız.
100 + 60 + 80 + 200 + 120 = 560 santimetrekare
Tarih: 2013-11-06 22:00:00 Kategori: Edebiyat
Kitaptan sorunu tarat hemen cevaplansın.
Yorum Yapx

 8 yıl önce
8 yıl önce
